what happens to the density of a liquid that is heated

Density

Densityis a measure of how much mass there is in a given volume or corporeality of space. The density of whatsoever substance is calculated by dividing the mass of the matter by the volume of the matter.

---

In Fig. 2.ii, volume is represented by boxes and individual particles of thing are represented by colored shapes.

• Box A has five spheres.
• Box B is the same size, and has the same volume every bit box A, only box B has x spheres.
• Box C has the same mass as box A, with 5 spheres, only box C has a larger volume than boxes A and B.
• Box D has the same volume and number of light-green spheres as office A, but also includes other types of matter than the rest of the boxes—ruby-red circles and blue cubes.

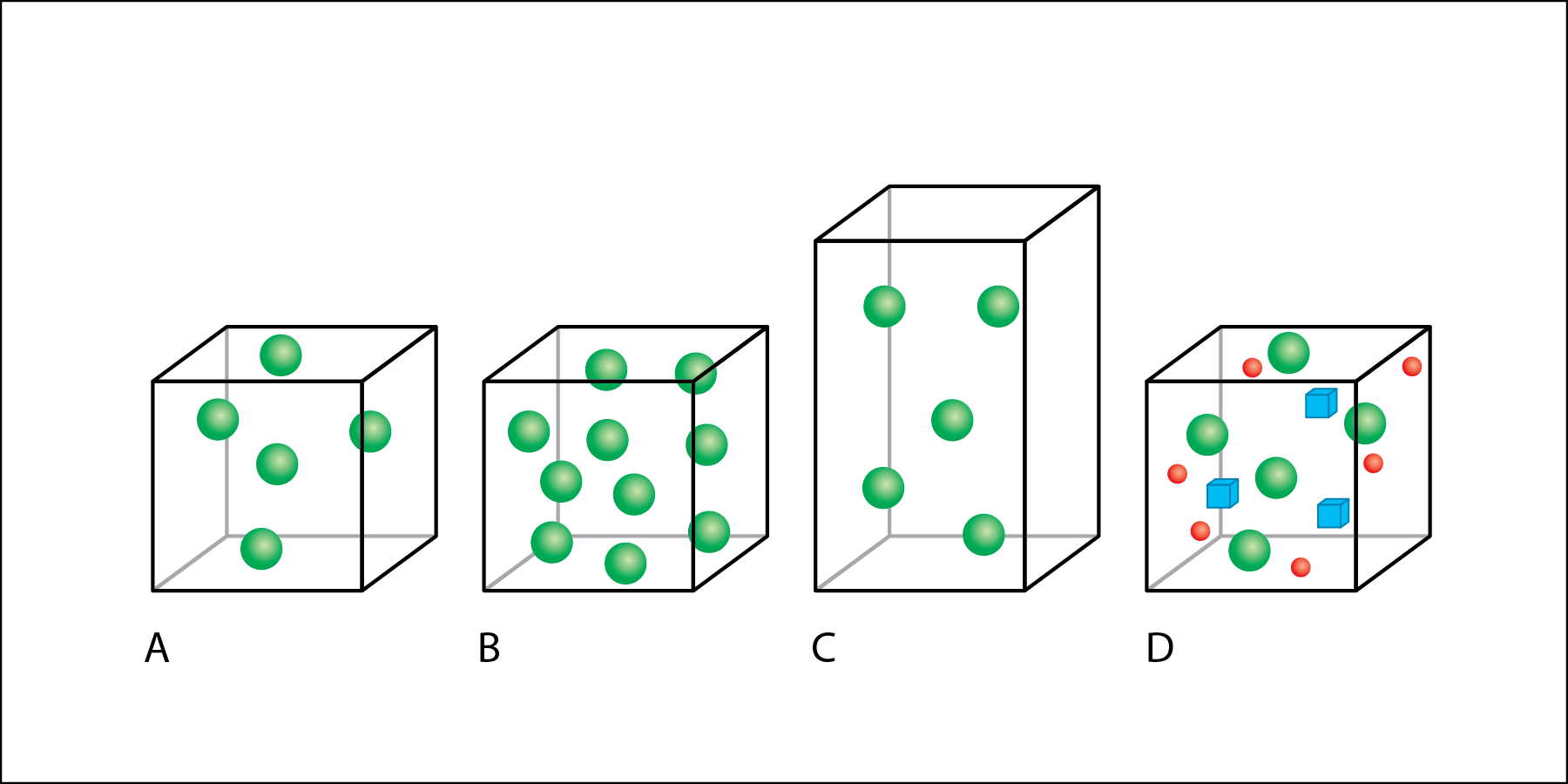
If the corporeality of matter is increased without changing the volume, then the density increases (Fig. 2.2 A to 2.2 B). If volume increases without an increase in mass, and so the density decreases (Fig. 2.two A to 2.2 C). Calculation additional matter to the same volume also increases density, even if the thing added is a dissimilar type of affair (Fig. 2.2 A to ii.2 D).

Salinity Affects Density

When salt is dissolved in fresh h2o, the density of the water increases considering the mass of the water increases. This is represented by the addition of red spheres and blue cubes to the box from Fig. ii.two A to Fig. 2.2 D. Salinity describes how much salt is dissolved in a sample of water. The more common salt there is dissolved in the water, the greater its salinity. When comparing 2 samples of water with the aforementioned volume, the water sample with higher salinity will have greater mass, and it will therefore be more dumbo.

Temperature Affects Density

The density of water tin also be afflicted by temperature. When the same amount of water is heated or cooled, its density changes. When the h2o is heated, it expands, increasing in volume. This is represented past the increase in the size of the box from Fig. 2.two A to 2.2 C. The warmer the h2o, the more space it takes up, and the lower its density. When comparing two samples of h2o with the same salinity, or mass, the water sample with the higher temperature volition have a greater book, and information technology volition therefore be less dense.

Relative Density

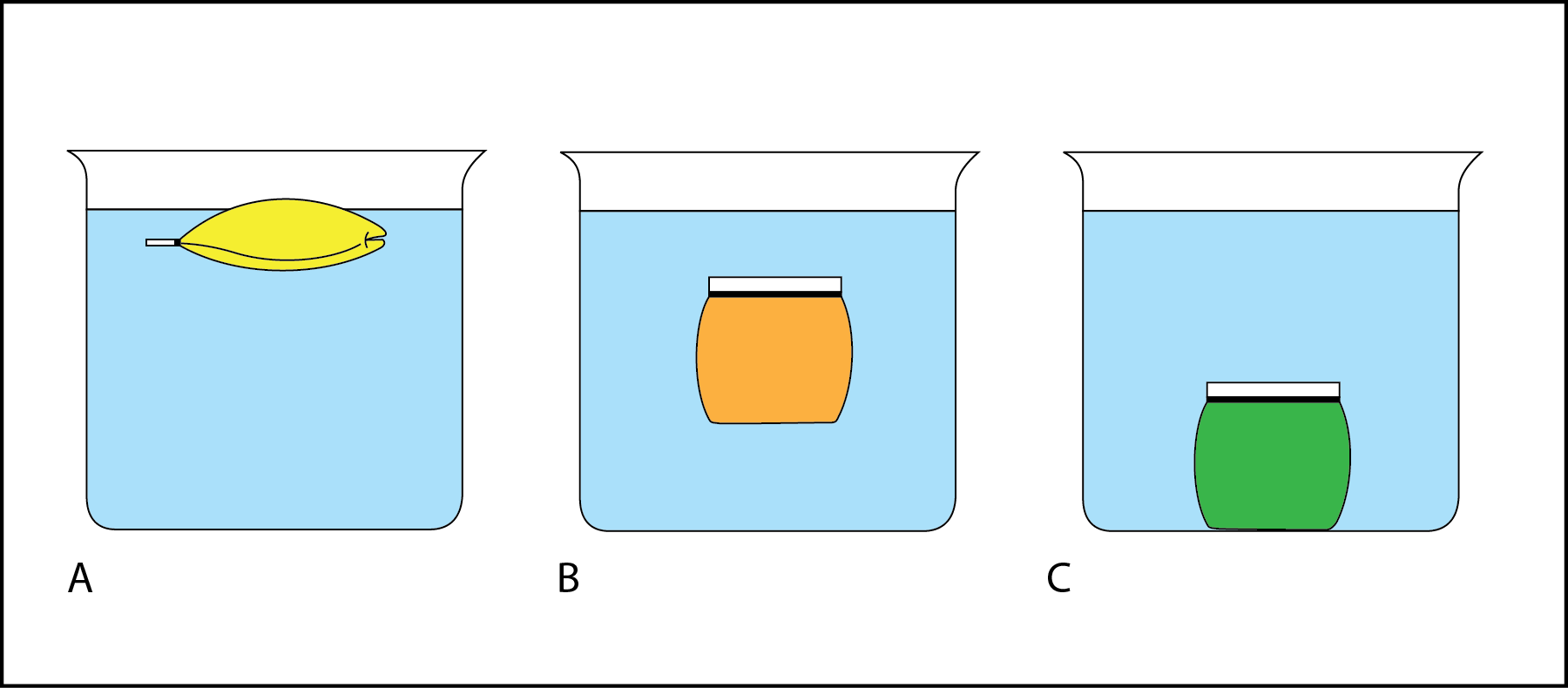
In Fig. 2.3, the beaker of liquid models a torso of h2o like the ocean or a lake. The pocketbook of liquid simulates a layer of water. The relative density of the liquid in the bag compared to the liquid in the chalice tin can be determined by observing whether the handbag sinks or floats.

• In Fig. 2.3 A, the bag rose to the top of the beaker and is now floating on the surface. The yellow liquid and the purse are less dense than the liquid in the beaker.
• In Fig. 2.iii B, the bag is floating in mid-water (subsurface floating). The orange liquid and the bag are equal in density to the liquid in the beaker.
• In Fig. 2.3 C, the bag sank to the bottom of the beaker. The dark-green liquid and the bag are more dumbo than the liquid in the beaker.

Activeness

Activity: Density Numberless

Examination the effects of salinity and temperature on the floating and sinking of liquid samples in bags.

Water Layers

If h2o masses have salinity or temperature differences, they volition form h2o layers because they have unlike densities. Water layers can sometimes be felt when pond. For example, on hot days the sun'due south rut tin make water at the surface noticeably warmer than the deeper, cooler water. The relative density of i h2o mass in relation to another determines whether a layer of water floats or sinks.

Density and Buoyancy

Density tin be determined by measuring the mass and book of an object. In the Density Bags Activeness, density was not calculated. Instead, relative density was determined by observing whether a purse of one liquid floated or sank in another liquid. A bag of liquid that sank was adamant to exist more than dumbo than the liquid in the beaker. A bag of liquid that floated was determined to exist less dense than the liquid in the beaker.

" championship="

Image past Byron Inouye

">

The motion of any object is due to forces , which are pushes or pulls. Vertical—upwards-and-down—motility of h2o masses in the ocean tin exist explained in terms of two forces. The gravitational force (G) of the earth pulls down and is proportional to the mass of an object. In Fig. two.five, the gravitational strength (K) is proportional to the mass of the red block. The gravitational force on an object is likewise called weight . The force due to gravity is greater on objects that are more massive, or weigh more than. The buoyant forcefulness (B) of water pushes up. In the third century B.C., the Greek philosopher Archimedes was the first to describe buoyancy. He observed that the book of water pushed out of a tub, or displaced, by an object was equal to the volume of the object. The buoyant strength of the water is equal to the weight of the water displaced. This concept is known as Archimedes' Principle , and it explains why objects sink or bladder. In Fig. ii.five, the buoyant force (B) is equal to the weight of the water displaced by the red block.

An object accelerates when the forces on that object are unequal. Although acceleration is ordinarily used to describe an object that is speeding up, the scientific definition of acceleration ways irresolute speed. An accelerating object can exist speeding up or slowing down. An object volition e'er move in the direction of the greater force. An object may advance downward (sink) or upwards (rising) in a body of h2o.

• Sinking is a downward vertical movement that occurs when the gravitational force (G) on an object is greater than the buoyant strength (B) supporting it (K > B).
• Ascension is the upward vertical movement that occurs when the gravitational force is less than the buoyant force (Yard < B).

If all of the forces on an object are balanced, at that place is no acceleration. In this instance, the object may not move—similar a volume sitting on a flat tabular array—or the object may move at a abiding speed—similar a auto traveling at a steady 80 kilometers per hour. In the water, an object might remain still either at the surface or within the water column.

• Surface floating occurs when an object stays at the surface, because the forces are balanced at the surface (Thou = B).
• Subsurface floating, or neutral buoyancy, occurs when an object maintains its position in mid-water, neither sinking nor ascension (Chiliad = B).

Iii cubes of the aforementioned size, but with dissimilar masses and thus different densities, are placed in 3 beakers of water (Fig. 2.half dozen). Because the cubes are identical in book, they displace the same amount of water. By Archimedes' Principle, the buoyant force (B) acting on each cube is equal. Buoyant force is represented in Fig. 2.6 as upward pointing arrows, indicating the h2o is pushing up on the cubes. These arrows are the same length for each of the cubes, indicating that the strength of the buoyant forcefulness acting on each cube is the same.

Because the masses of the cubes are non equal, the gravitational forcefulness (G) acting on each cube is dissimilar. Gravitational force is represented in Fig. ii.six every bit downward pointing arrows, indicating the gravitational strength is pulling down on the cubes. These arrows are unlike lengths for each cube, indicating that the amount of the gravitational force is different for each cube. The downwardly pointing arrow in Fig. 2.half dozen A is the shortest, indicating that the yellow cube has the least mass and is the least dense. The downward pointing arrow is the longest in Fig 2.6 C, indicating that the green cube has the most mass and is the well-nigh dense.

The density of the cube relative to the density of h2o determines if the cube volition bladder, sink, or be neutrally buoyant:

• If the density of the cube is less than the density of the water, gravitational strength will exist less than the buoyant force (G < B), and the object will rise to the surface (Fig. 2.6 A).
• If the density of the cube is equal to the density of the h2o, the cube will bladder in middle of the cavalcade of water considering the gravitational force and buoyant force are counterbalanced (G = B). This cube is neutrally buoyant (Fig. 2.vi B).
• If the density of the cube is greater than the density of the water, the cube will sink considering the gravitational force is greater than the h2o's buoyant forcefulness (Thousand > B) (Fig. ii.6 C).

baileyconsento.blogspot.com

Source: https://manoa.hawaii.edu/exploringourfluidearth/physical/density-effects/density-temperature-and-salinity

Share this post